Les pièges de l’utilisation des chiffres

Quelque soit l’espace médiatique, les chiffres sont utilisés partout pour appuyer les discours car ils ont la réputation de montrer LA vérité. Or les chiffres ne sont pas neutres et même avec la meilleure volonté, ils peuvent receler des erreurs et amener à se faire de fausses idées, voire orienter volontairement l’opinion des lecteurices. Cette fiche reprend les erreurs les plus courantes concernant l’utilisation des chiffres dans le champs de l’actualité. Elle est complémentaire de la fiche sur les chiffres dans l’actualité qui s’intéressera pour sa part à l’analyse des chiffres dans les médias du point de vue du discours. Nous parlerons donc dans cette fiches de l’analyse des corrélations, des principaux paradoxes mathématiques connus dans l’utilisation de statistique et enfin des biais cognitifs propres à la construction de statistiques.

Corrélation

La corrélation est une caractéristique reflétant l’existence d’une relation entre deux variables. Si deux événements se produisent dans un même contexte, on considère qu’ils sont liés. Par exemple, une personne qui a le diabète va avoir un taux de sucre élevé et ressentir une faim excessive. Les deux facteurs sont liés, et proviennent d’un même contexte qu’est la maladie du diabète.

Une confusion est très fréquemment retrouvée entre corrélation et causalité. La causalité souligne une relation de cause à effet entre les deux événements. Cela implique qu’un événement entraîne l’autre. Si l’on reprend notre exemple de la personne atteinte de diabète, le taux de sucre élevé n’entraîne pas le sentiment de faim excessive, et vice versa. Ce sont des faits liés mais pas par une causalité. Également, à l’œil nu, notre cerveau peut nous laisser croire qu’il existe une corrélation quand il n’y en a pas. Il est important de bien noter qu’une relation entre deux événements ne se résume pas par une tendance de progression similaire.

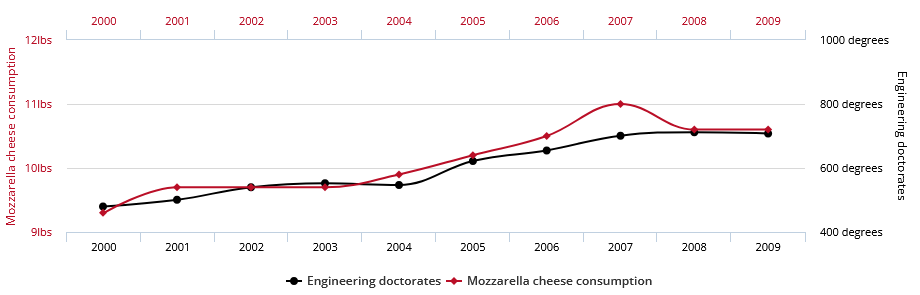
Ce graphique extrait du site http://tylervigen.com/spurious-correlations met en parallèle la consommation de mozzarella par habitants aux US et le nombre de diplômés de doctorat en ingénierie civile par an. Visuellement, l’évolution similaire peut nous tromper et laisser supposer un lien entre les deux bien que cette corrélation semble absurde. En revanche, si l’on avait le même graphique avec cette fois la taille du père et la taille de l’enfant, nous pourrions considérer qu’il existe une corrélation entre la taille d’un enfant et celle de son père. Il resterait alors à prouver la causalité.

Pièges mathématiques

Le paradoxe de Simpson

Le paradoxe de Simpson est un paradoxe mathématique assez connu qui peut causer pas mal de difficulté lors de l’analyse de chiffres si on y fait pas attention. En effet il est utilisé lorsqu’on observe dans deux groupes distincts une tendance, qui s’inverse quand les deux groupes sont rassemblés. Ceci est possible à cause de deux éléments non pris en compte lors de la première analyse qui sont :

Un facteur de confusion, c’est à dire un élément qui n’est pas dit explicitement au début mais qui influe directement sur ce qu’on essaye d’observer, par exemple l’âge sur la mortalité, en effet difficile de vérifier si les gens meurt plus ou moins de quelque chose si on ne prends pas en compte le risque de mortalité par rapport à leur tranche d’âge.

Une distribution non homogène, c’est à dire que dans les deux groupes, il n’y ai pas le même nombre de personnes concernées par le facteur de confusion. Si on reprend l’âge, qu’il y ai plus de personne âgées (donc avec plus de chance de mourir) dans un groupe que dans l’autre.

Si on observe une distribution non homogène et un facteur de confusion, on peut alors facilement se retrouver à avoir des analyses incohérentes et donc amener à des conclusions fausses.

Pour donner un exemple un peu moins dramatique que la mortalité on peut observer par exemple le nombre de parties gagnées par 2 personnes :

Alex et Morgan jouent au même jeux en ligne. Chaque mois iels comptent le nombre de fois ou iels réussissent un niveau commencé pour pouvoir faire un concours de la personne ayant le meilleur taux de réussite du jeu. Le premier mois Alex fini 60 niveaux sur 100, Morgan en fini 9 sur 10
Alex a fini 60% des niveaux tentés alors que Morgan 90%.
Morgan a donc fini le plus grand pourcentage de niveaux.

Le deuxième mois, Alex fini seulement 2 niveaux sur les 10 qu’elle commence, Morgan en fini lui 35 sur les 100 commencés.
Alex a cette fois fini 20% des niveaux qu’elle a commencé alors que Morgan en a lui fini 35%

Le troisième mois, Alex fini 30 niveaux sur les 50 qu’elle commence. Morgan lui devient plus raisonnable et fini 30 niveaux les 40 qu’il tente. Morgan a encore une fois le meilleur pourcentage de niveaux car il en a fini 75% alors qu’Alex elle en a fini seulement 60%.

C’est donc encore Morgan qui a fini le plus grand pourcentage de niveaux les 3 mois du concours. Or si on fait un tableau des résultats, au final on se rend compte que c’est Alex qui a en réalité le meilleur taux de réussite.

	Mois 1	Mois 2	Mois 3	Bilan
Alex	60/100 = 60%	2/10 = 20%	30/50 = 60%	92/160 = 57,5%
Morgan	9/10 = 90%	35/100 = 35%	30/40 = 75%	74/150 = 49,33%
Gagnant·e	Morgan	Morgan	Morgan	Alex

Ici le facteur de confusion est le nombre de niveaux commencés qui n’est pas le même suivant les mois pour les deux personnes, ce qui est donc une distribution non homogène. On a ainsi tout les éléments du paradoxe. Cet exemple est inspiré de l’article Wikipédia sur le paradoxe de Simpson et d’un article de Science Étonnante sur ce sujet.Dans le cadre médiatique ce paradoxe peut être utilisé sur les chiffres de l’immigrations par exemple, ou dans le cas d’analyse d’études de médecine et peut donc amener à changer son point de vu sur des sujets importants.

Médiane VS moyenne

Dans l’actualité il est souvent utilisé la notion de moyenne. La moyenne se calcule en additionnant toutes les valeurs d’un ensemble puis en divisant le total par le nombre de valeurs que contient cet ensemble. Par exemple pour calculer la moyenne scolaire d’un élève on va prendre les notes qu’iel a obtenu dans toutes les matières, les additionner et diviser par le nombre de matière. Dans certains cas la moyenne est un outil très pertinent, mais dans d’autres elle peut ne pas du tout être représentative. C’est par exemple le cas dans la répartition des richesses ou des salaires. Dans ces cas la moyenne fait complémentent disparaître les inégalités entre les salaires les plus bas et les plus haut. De plus elle n’est pas du tout représentative de la majorité de la population.

Dans ces cas un autre indicateur existe : la médiane. La médiane, va indiquer la valeur qui va séparer le groupe en exactement deux parties égales. Le salaire médian français représente par exemple le salaire qui divise en deux parties égales les salaires français. Il y a donc autant de français·e·s qui touchent moins que le salaire médian, que de français·es qui touchent plus.

Il est donc intéressant de regarder avec attention les indicateurs donnés et quand c’est possible de vérifier les données brutes pour pouvoir se faire sa propre idée. Pour en savoir plus sur ces deux indicateurs, Une vidéo super intéressante de la chaîne YouTube la statistique expliquée à mon chat, reprends le cas des salaires pour montrer les écueils d’une moyenne.

Analyse de la distribution

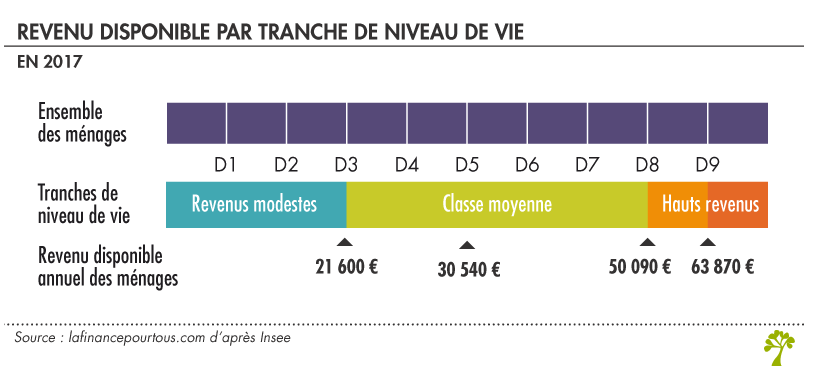
Pour aller plus loin dans la compréhension des chiffres et proposer des présentations claires des chiffres, un autre outil que la médiane et la moyenne peut être utilisé en complément ou à la place de l’un des deux : la distribution. La distribution représente la répartition des chiffres sur un axe donné et sa division en un certains nombres de portions égales qu’on les appelle quantile. Certains ont un nom spécifique en fonction du nom de portions (quartile -> 4, quintile -> 5, décile -> 10, centile -> 100). Cette technique permet de facilement visualiser les variations d’une courbes et de pouvoir donner des informations rapidement à la personne qui lit le graphique. Dans ce graphique les déciles sont représentés par les rectangle violet, chaque rectangle représentant 10% de la population (source).

Biais cognitif

Le biais de la loi des petits nombres

La loi des petits nombres est un biais cognitif qui pousse les individus à croire qu’un petit nombre d’observations peut refléter fidèlement la population générale.

Par exemple, si on on compte à une réunion 70% de femmes et qu’on utilise cette proportion de 70% de femme pour deviner le nombre de femmes dans le monde, on aurait tendance à penser qu’il y a donc il y a 70% de femmes dans le monde. Cette impression est fausse car elle n’est pas représentative de la réalité, ni du hasard de l’échantillon. Les personnes participant à cette réunion sont des personnes plutôt jeunes, étudiantes donc éduquées vivant proche de l’événement ce qui influence fortement la répartition des genres. On ne peut donc pas en conclure une généralité. De la même façon ce n’est pas parce que nous avons guérit alors que nous utilisions un remêde de grand-mère que celui-ci fonctionne réellement et pour toutes la population. c’est pour cela qu’en médecine de nombreux tests sont réalisés afin de savoir si oui ou non un traitement à un effet bénéfique.

Afin de ne pas tomber dans ce biais, par exemple en lisant un sondage, il est important d’analyser le nombre de personnes interrogées et comment elles l’ont été, de même pour tout autre analyse statistique.

Le biais de la régression vers la moyenne

Ce biais se passe lorsque nous ne regardons que 2 mesures. Il s’appui sur l’idée qu’avec 2 mesures on peut déduire une tendance. Or, en statistique, la régression vers la moyenne décrit le phénomène suivant : si une variable est extrême à sa première mesure, elle va généralement se rapprocher de la moyenne à sa seconde mesure. Si elle est extrême à sa seconde mesure elle va tendre à être proche de la moyenne à sa première mesure. Avec seulement 2 mesures, on se retrouve donc avec une moyenne biaisée, il faudrait idéalement une beaucoup plus grande quantité de mesures.

Par exemple, si l’on obtient une mauvaise note en ayant révisé à un contrôle et une bonne en ayant pas révisé, on peut croire que ne pas réviser nous aiderait à avoir de meilleures notes. On ne prend alors pas en compte le hasard et les fluctuations aléatoires possibles. On a peut-être eu de la chance lors de l’examen où on n’a pas révisé.

La solution afin de contrer ce biais est d’analyser sur le long-terme au lieu de ne regarder uniquement quelques valeurs. La moyenne d’un grand nombre de mesures permet de conclure à une tendance, car avec énormément de mesures, on rejette des variations qui peuvent être aléatoires. Il faut également faire attention aux possibles facteurs confondants : si on a mal dormi lors du contrôle où on a révisé, cela a pu baisser notre note.

Le biais d’ancrage

En psychologie, le biais d’ancrage désigne la difficulté que l’on rencontre à se départir de sa première impression. En se focalisant sur une première information, une première valeur ou un premier élément, l’esprit n’arrive plus à apprécier et prendre en considération les nouvelles informations, les nouvelles valeurs ou à envisager d’autres choix.

C’est pourquoi on dit que la première impression est très importante. Car elle reste le plus souvent dans la tête des gens qu’on rencontre, et cela est très difficile de s’en détacher.

Les vendeurs vont également donner par exemple un prix très élevé pour un produit, pour qu’on le surévalue. Ainsi, faire descendre son prix entraînera moins de pertes. La solution est de donner d’abord une valeur soi-même et ainsi, « ancrer » une valeur avant le vendeur. On peut ensuite alors négocier.

Le biais de confirmation

Le biais de confirmation d’hypothèse (ou biais de confirmation) est un biais cognitif qui fait que les êtres humains privilégient les informations qui confortent leurs opinions.

Par exemple, un climato-sceptique qui s’appuie sur 4 jours de froid en mai pour remettre en cause toutes les études scientifiques qui mettent en évidence le réchauffement climatique lié à l’activité humaine et pas forcément visible à l’oeil nu. Dans cet exemple en plus d’utiliser le biais de la loi des petits nombre, la personne nie toute la recherche scientifique prouvant le contraire . Un autre exemple pourrait être les personnes cherchant à se renseigner sur un événement historique et n’acceptant que les thèses allant dans leur sens. Ou encore les fans refusant de croire à un crime commis par une star et cherchant tous les moyens de conforter leur opinion que cette personne n’est pas si mauvaise.

Ce bais est l’un des plus courant dans les cercles de pairs et peut mener à adhérer à diverses théories du complot. Aussi est-il préférable de ne rien prendre pour acquis et de toujours faire des recherches complémentaires autours des sujets les plus important pour vous.

Le biais de cadrage

Le biais de cadrage (ou effet de cadrage) désigne l’influence importante que peut avoir la formulation d’une question ou d’un problème sur la réponse qui y est apportée. Il montre à quel point l’être humain est influençable.

Par exemple, une épidémie sévit dans le pays, une équipe de médecins propose deux programmes pour traiter le problème. Avec le programme A, 400 personnes mourront. Avec le programme B, il y a une chance sur 3 de sauver 600 vies.

Face à cet énoncé, 72% des participants à l’étude ont choisi le programme B. Or le résultat obtenu est identique dans les deux cas : 200 personnes seront sauvées, 400 mourront. Autre exemple : un gouvernement lance un référendum sur la réforme des retraites. La question est posée comme le fait d’appliquer ou non la réforme d’augmentation des cotisations à l’ensemble des citoyen·ne·s. Cette réformer aurait pour but de réduire les déficits, ne pas l’applique reviendrait donc à laisser le système créer la faillite de l’état. Or, ce gouvernement choisit de ne pas considérer l’option d’augmenter les cotisations des plus fortunés seulement et pas de l’ensemble de la population.

Le biais de représentativité

Le biais de représentativité est la tendance à fonder son jugement ou à prendre une décision à partir d’un nombre limité d’éléments que l’on considère comme représentatifs d’une population beaucoup large.

On peut penser qu’une personne en échec scolaire gagnera moins bien sa vie qu’une personne qui a bien réussi ses études. Or statistiquement, les filles réussissent mieux leurs études mais sont moins payées que les hommes.

Ressources pour aller plus loin :